可解释性推荐系统
背景
在出推荐结果的同时产出一个理由,告诉用户这个item为啥要推荐给你~

大致的概念总结起来是这么一个图:
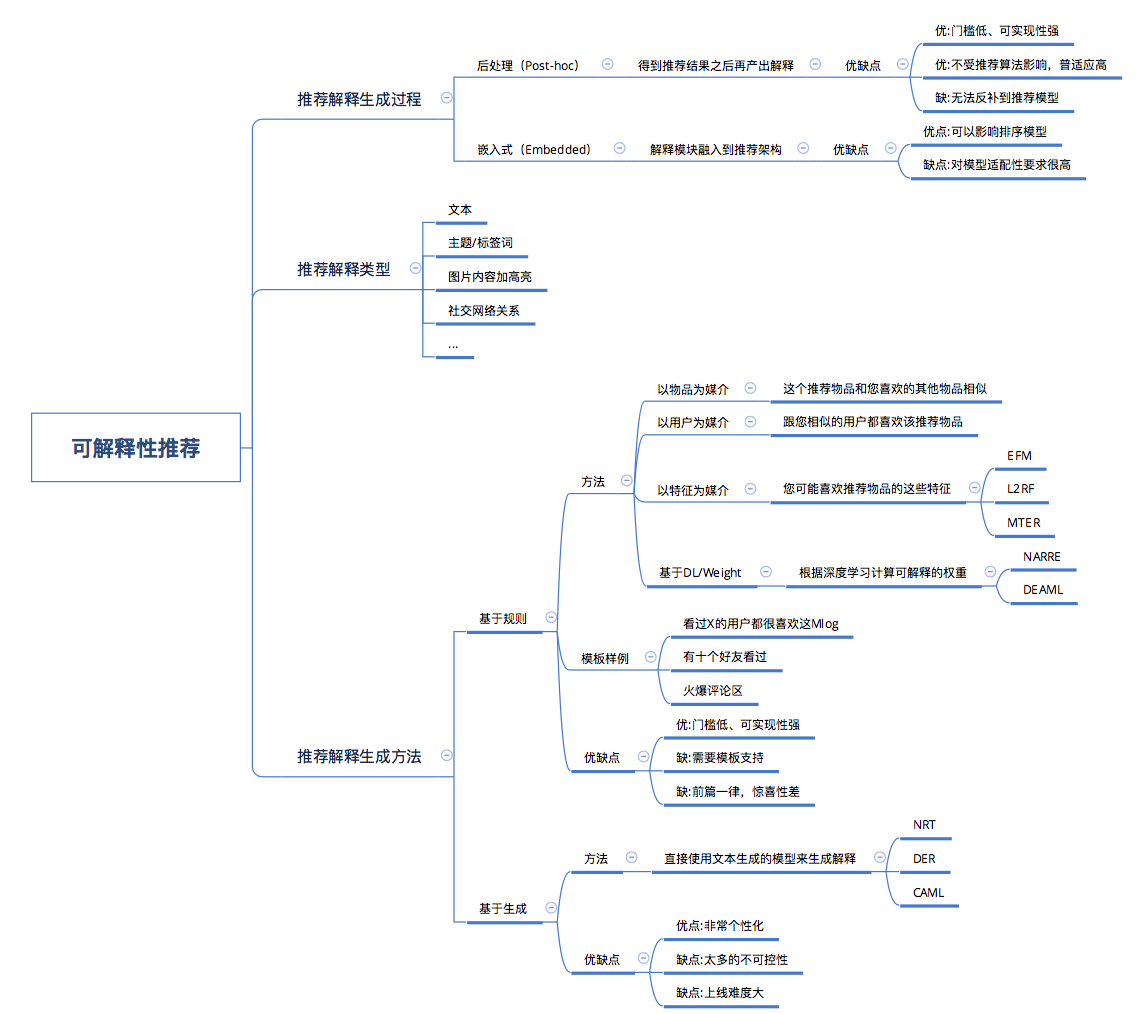
下面列举了一些最近自己调研的方法和理解
矩阵分解方法
EFM
经典的矩阵分解方法可以根据 User-Item 的行为矩阵进行分解,然后得到User向量和Item向量之后进行推荐,而EFM在矩阵分解的基础上加入了 User/Item的显式特征矩阵,使得在推荐结果上可以拿到对应的显式特征,从而进行推荐的可解释性,当然,这里的特征一般指的是Aspect的属性。
EFM在关键idea时推荐的同时给到用户比较关心的特征,在paper的场景中,给到用户评分行为,同时评分时会得到相应的评价文本,
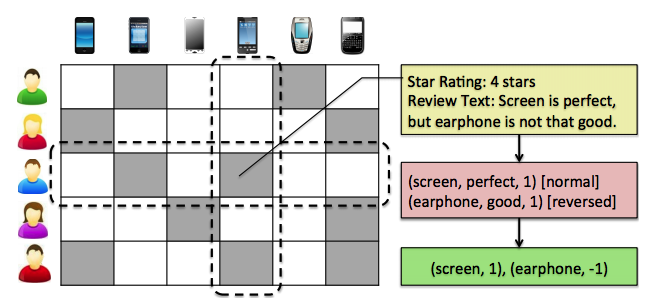
这样就是这样的一个评分矩阵,其中左侧是用户的评分行为,左侧有对应的评价文本,作者对该评价文本进行情感分析,比如可以得到(screen,1),(earphone,-1)的情感,这里的screen和earphone这些属性就可以作为对应的”特征”,因为根据评论情况,用户对于”特征”会有偏好,同时Item方面也会对不同的”特征”差异。
因此借助用户的评论对其情感分析,可以构建User-Feature和Item-Feature的显示特征矩阵,
其中对于User-Feature的填充值为:
$$ X_{i,j}=\left\{
\begin{aligned}
0 & \quad if \quad u_i \quad not \quad mention \quad feature \quad F_j \\
1+(N-1)(\frac{2}{1+e^{-t_{i,j}}}-1) & \quad else \\
\end{aligned}
\right.$$
其中N表示$t_{i,j} \in [1,N]$ 为实际评分分数,为$N$为最大评分分数
同时对于Item-Feature的填充值为:
$$ Y_{i,j}=\left\{
\begin{aligned}
0 & \quad if \quad p_i \quad not \quad reviewed \quad feature \quad F_j \\
1+\frac{N-1}{1+e^{-k \cdot s_{i,j}}} & \quad else \\
\end{aligned}
\right.$$
其中$k$为该$F_j$在$p_i$上出现的次数,同时$s_{i,j}$就是对应的平均评分数
因此可以用X来表示用户的显式特征矩阵,Y来表示Item的显式特征矩阵,利用矩阵分解,可以有
$X = U_1 V ^T \quad Y = U_2 V^T$
这样$U_1,U_2$分别为用户和item对应的显式向量矩阵,而$V$为特征的显示向量矩阵,如果根据这两个矩阵直接进行推荐,其优化函数为:
$$ \underset{U_1,U_2,V}{minimize} \left \{ \lambda_x \parallel U_1V^T - X \parallel _F^2 + \lambda_y \parallel U_2V -Y \parallel _F^2 \right \} , st. U_1 \in R^{m \times r},U_2 \in R^{n \times r},V \in R^{p \times r}$$
这边的$\lambda_x$和$\lambda_y$是正则项因子,同时$r$就是为显示特征的向量大小.
而上面的式子仅为用户行为在显式特征部分的表示,这些显式特征并无法全部表示用户的行为(至少丢掉了用户对应item的偏好),因此还需要再加入用户的隐式偏好。
这边使用${r}’$来表示隐式特征向量的大小,,其中使用$H_1$和$H_2$分别来表示用户和Item的隐式偏好矩阵,其中A为用户对于Item的评分矩阵,这里另$P=[U1,H1]$和$Q = [U2,H2]$,他们以拼接的方式来表示用户和Item的全部信息,则希望$$PQ^T \approx A$$。
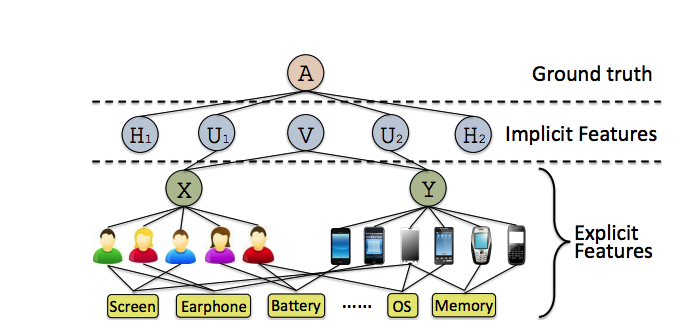
因此最终的优化函数为
$$ \underset{U_1,U_2,V,H_1,H_2}{minimize} \left \{ \parallel PQ^T - A \parallel _F^2 + \lambda_x \parallel U_1V^T - X \parallel _F^2 + \lambda_y \parallel U_2V -Y \parallel _F^2 + \\ \lambda_u (\parallel U_1 \parallel^2 + \parallel U_2 \parallel^2 ) + \lambda_h (\parallel H_1 \parallel^2 + \parallel H_2 \parallel^2 ) + \lambda_v \parallel V \parallel^2 \right \} $$
由于该式子无法直接优化,作者是通过每个矩阵依次迭代进行优化的,具体可以参考paper
这边当$r=0$的时候,其实就是回归到了普通的用户行为矩阵推荐。
考虑到用户的显式特征信息,在实际推荐时,会选取用户最关心的$k$个显式特征$C = { c_1,..,c_k }$然后进行item的得分计算:
$$R_{i,j} = \alpha \cdot \frac{\sum_{c \in C} \tilde{X}_{ic} \cdot \tilde{Y}_jc }{kN} + (1-\alpha) \tilde{A}_{i,j}$$
这边的$\alpha$就是取显式特征还是考虑综合行为的一个平衡因子
再记得得到top的Item列表之后,再选取最关心的显式特征,套用预定好的模块即可展现推荐理由:

LRPPM
LRPPM模型其实是EFM的一个泛化或者增强版本,主要做了下面两个方面的改进:
- 从
User-Feature和Item-Feature的显示特征矩阵直接衍化到了User-Item-Feature的立体 - 使用learning-to-rank的方式从
Pointwise到PairWise的变更
另外为了解决单个item上用户评论的稀疏性,LRPPM还提供到了类目测的模型
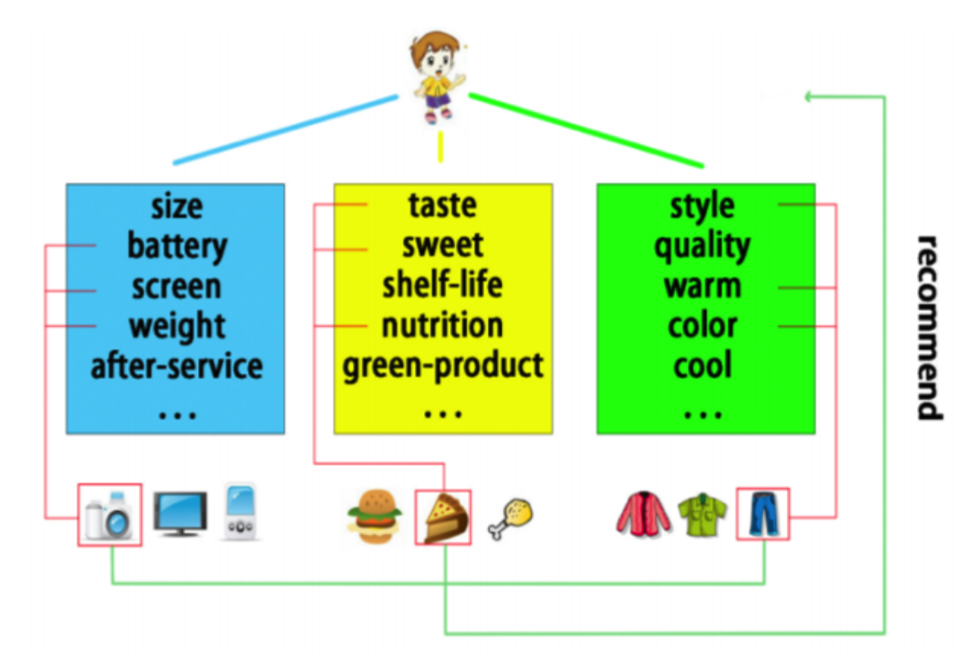
该三元立体的式子表示为:
$$\hat{T}_{uif} = \sum_{k=0}^{K-1} R_{uk}^U \cdot R_{fk}^{UF} + \sum_{k=0}^{K-1} R_{ik}^I \cdot R_{fk}^{iF} + \sum_{k=0}^{K-1} R_{uk}^U \cdot R_{ik}^I$$
该式子的含义就是用户$u$对于物品$i$在某个特征上$f$的感兴趣得分,值得注意的时候,对于特征$f$的向量,作者将$U$和$I$上面的特征给分来表示了。在进行优化的时候,作者参考了$BPR$的损失函数,他认为这个可以理解是一个pairwise的排序场景,也就是用户对于$ui$上的感兴趣特征分数比不感兴趣的高即可,所以可以有得到
$$\hat{T}_{uif_Af_B} = \hat{T}_{uif_A} - \hat{T}_{uif_B}$$
其中$f_A$表示用户感兴趣的特征,而$f_B$则一般可以用 用户 没观察到的特征
这样则其优化函数为
$$\hat{\theta} = \underset{\theta}{argmax} \sum_{u \in U} \sum_{i \in I} \sum_{f_A \in F^+} \sum_{f_B \in F^-} \text{log} \sigma (\hat{T}_{uif_Af_B}) -\lambda_{\theta} \parallel \theta \parallel_F^2$$
其实就是一个表示的 BPR的损失函数
与EFM一样,LRPPM模型也会集成CF进行排序,这样其最小化目标就为:
$$ \underset{\theta}{min} \sum_{u \in U} \sum_{ i \in I} (A_{ui}- R_u \cdot R_i)^2 -\lambda \sum_{u \in U} \sum_{i \in I} \sum_{f_A \in F^+} \sum_{f_B \in F^-} \text{log} \sigma (\hat{T}_{uif_Af_B}) + \lambda_{\theta} \parallel \theta \parallel_F^2$$
同时刚刚有提到,其实单个用户对于某个物品的评论是很稀疏的,这样导致整个特征立方体非常稀疏,为了解决这个问题,上述的公式可以很方便的转为基于”类目”的理论,因为往往在同一个类目下的不同物品都会有项目的特征,所以转为”类目”级别之后这个立方体为”User-Categroy-Feature”,式子更改为这样:
$$\hat{T}_{ucf}^* = \sum_{k=0}^{K-1} R_{uk}^U \cdot R_{fk}^{UF} + \sum_{k=0}^{K-1} R_{ck}^C \cdot R_{fk}^{cF} + \sum_{k=0}^{K-1} R_{uk}^U \cdot R_{ck}^C$$
在最小化目标函数上做相应的替换和变更即可.
MTER
MTER这篇paper最大的idea就是在之前三元立体的基础上新增了一位 关键词(Opinionated word),类似于 价格-高,颜色-鲜艳
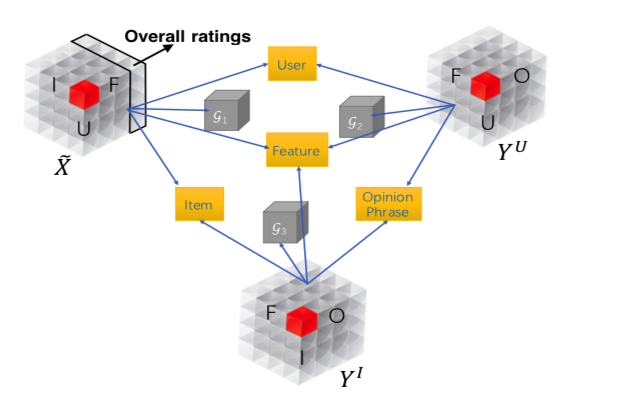
因此整个场景就可以模型化为一个四维的矩阵(U:用户,I:物品,F:特征,O:Opinion)
这里考虑到四维矩阵的相乘复杂度太高,所以作者将其分成了三个三维的矩阵:
- $\hat{X}$:
U-I-F - $\hat{Y}^U$:
U-F-O - $\hat{Y}^I$:
I-F-O
最终的优化公式为:
$$\underset{\hat{X},\hat{Y}^U,\hat{Y}^I}{min} \parallel \hat{X} - \tilde{X} \parallel_F + \parallel \hat{Y}^U - \tilde{Y}^U \parallel_F + \parallel \hat{Y}^I - \tilde{Y}^I \parallel_F$$
深度学习方法
NARRE
这边的思想其实很简单,将用户和Item的评论文本特征灌入的算分模型,同时借助Attention机制来获取权重最高的评论来作为推荐
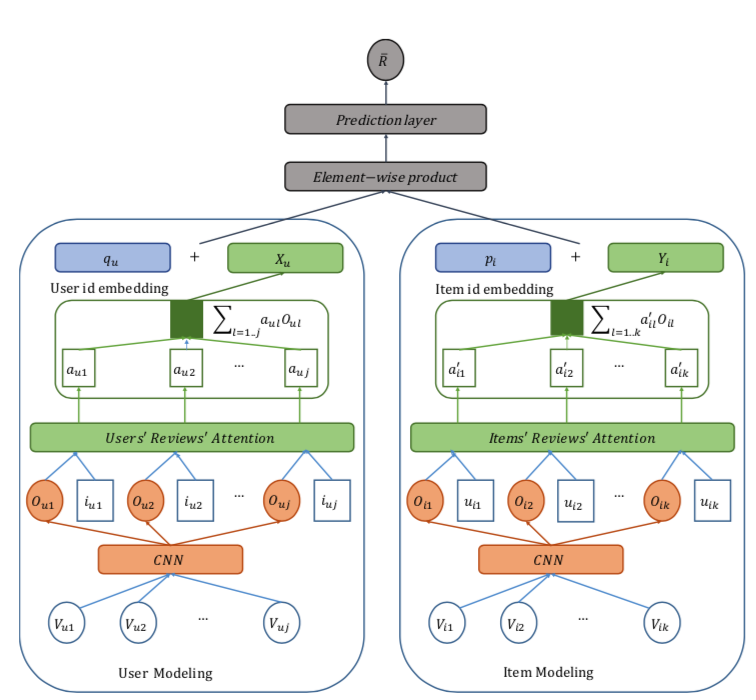
这边单个评论经过CNN进行embedding之后,与发表评论的user或者承载评论的item进行Attention是该paper的核心:
$$\hat{a}_{il} = h^T \text{ReLu}(W_oO_{il} + W_u u_{il} + b_1) + b_2$$
这样每条评论的权重可以经过softmax
$$ a_{il} = \frac{\hat{a}_{il}}{\sum exp(\hat{a}_{il})} $$
其中$O_{il}$表示评论的文本向量,$u_{il}$表示发表该评论用户,根据他们进行Attention之后按权重聚合得到$Y_i$作为整个Item的整体评论Embedding
同时用户产生的评论用类似的方式产生$X_u$,
最终使用$(q_u+X_u) \odot (p_i+Y_i)$点积的方式进行计算用户评分,其中$q_u$和$p_i$分别代表使用评论矩阵MF分解得到的用户和Item的向量
根据模型中$a_{il}$的权重即可来代表该Item最重要的评论进行推荐时展现

不过我觉得这部的Attention中并没有加入当前待排序用户的特征,所以$a_il$在不同的用户下应该都是同一个,因此评论并没有做到用户级别的个性化 -_-
NRT
NRT的作者在使用普通矩阵分解评分的时候,利用隐向量的来进行tips文本序列的生成
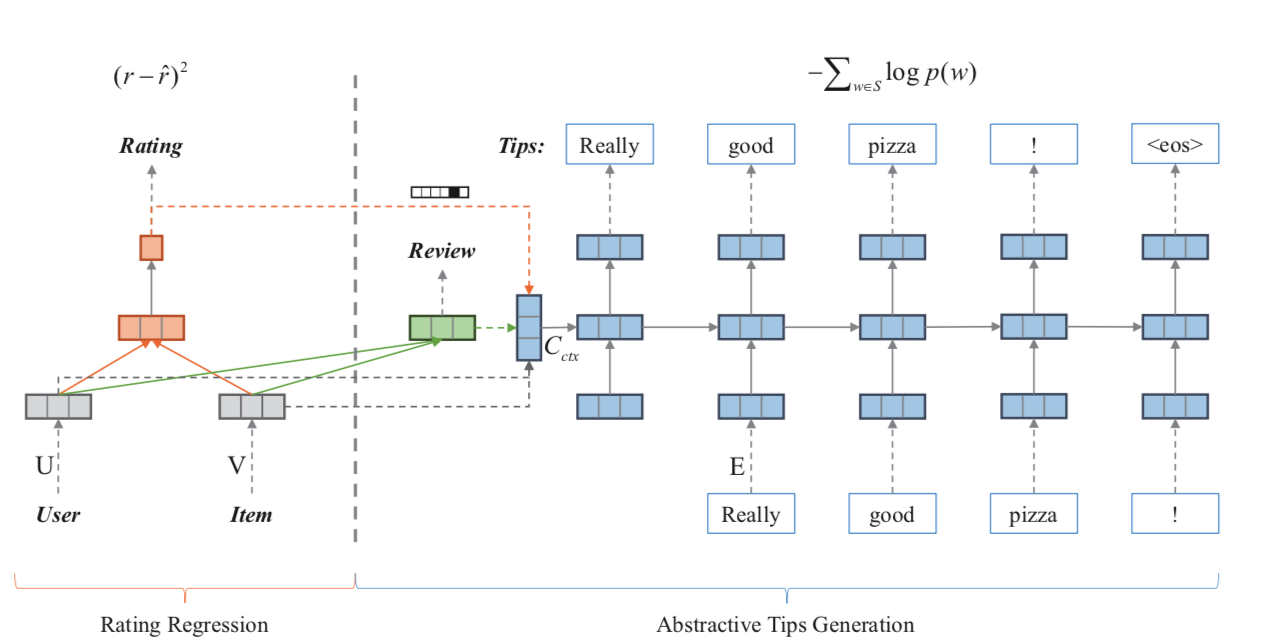
而在序列生成时使用了比较经典的GRU架构,而生成最关键的就是初始化的输入,NRT他是这么构造的
- $u$:用户的隐向量
- $v$:
Item的隐向量 - $\hat{r}$: 计算得分的onehot向量,比如总分5分,当前计算4.3分,则为$\{0,0,0,1,0\}$
- $h_L^c$: 可以使用非常简易的生成方法:通过多层感知机之后得到最后一层$h_L^c$,该层映射之后的softmax的值$\hat{c}$来拟合真实评论文本的词分布$\sum c^k \text{log} \hat{c}^k$,该数据在训练时有groundtruth,在预测时只需要inference即可
因此最终的初始化向向量输入为:$$h_0^s = tanh( W_uu + W_vv + W_r \hat{r} + W_c h_L^c + b)$$
该初始化向量其实含有信息量还是太少了,应该实际生成的效果相对来说还是比较差的
CAML
CAML在解释生成时的关键是要对用户和item之间进行深层次的交互并进行显式的建模,因此他是在序列生成的初始输入上针对NRT做了很大的改进,CAML的核心是根据用户和Item的评论进行多层的Co-Attention,包含评论级别和评论的属性级别,因此最终的生成还能进行属性进行控制
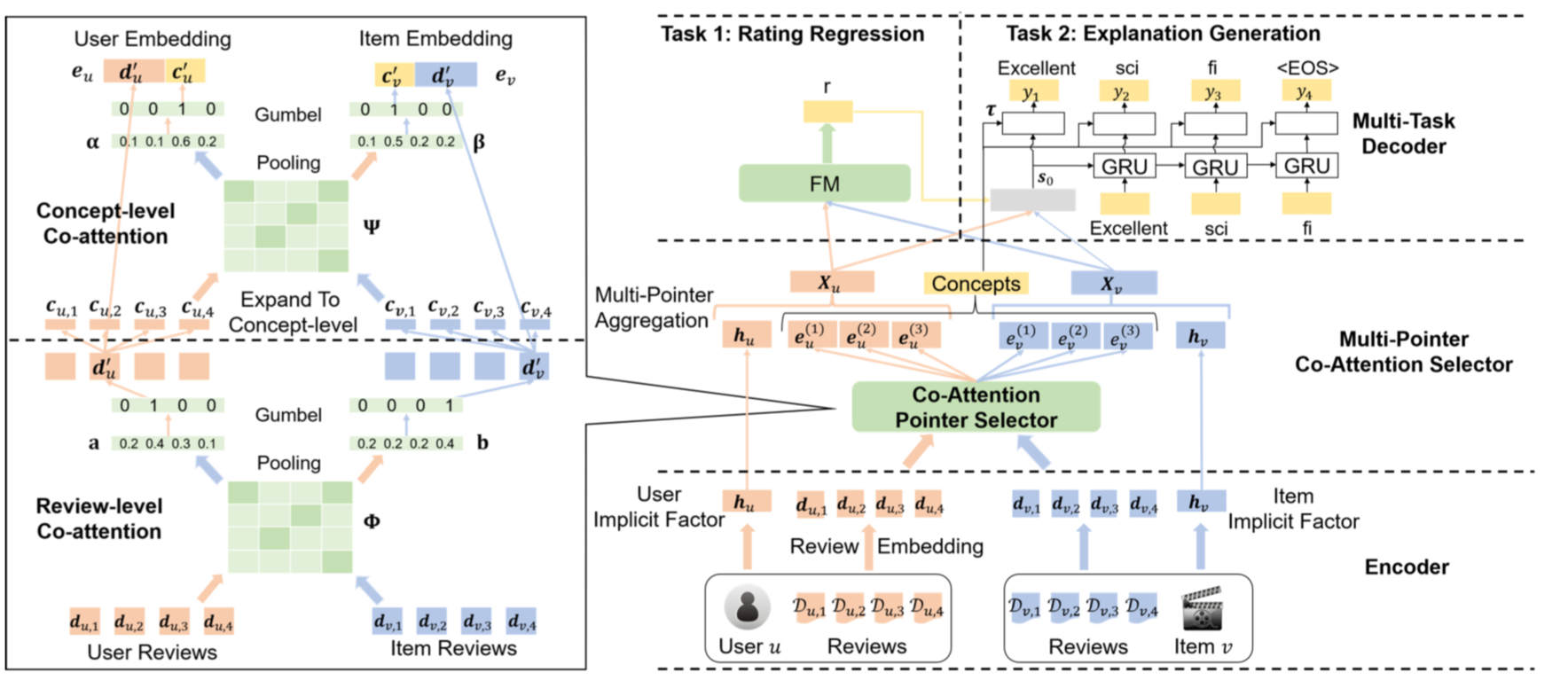
多层的Co-Attention是这样的:
- 根据用户和
Item的评论文本向量进行Co-Attention:$$\phi_{i,j} = F(d_{u,i})^T W_d F(d_{v,j})$$ - 同时取得用户和
Item测各条评论最重要的得分$$a_i = \underset{j=1…l_d}{max} \phi_{i,j} , b_j = \underset{i=1…i_d}{max} \phi_{i,j}$$ - 这边然后使用
Gumbel-Softmax函数得到最终的评论$$q_i = \frac{exp(\frac{a_i+g_i}{\tau})}{\sum exp(\frac{a_i+g_i}{\tau})}$$ - 然后可以得到用户和
Item的重要评论${d}’_u$和${d}’_v$ - 这些评论自身都有他们对应的属性(Concept) $c$,这些$c$按照类似
1-4的步骤记得最终这两条评论各自最重要的属性${c}’_u$和${c}’_v$ - 此时将他们向量进行拼接起来即可代表用户和
Item的评论偏好$e_u = [{d}’_u,{c}’_u]$和$e_v = [{d}’_v,{c}’_v]$ - 由于用户或者
Item可能不止对意向评论进行偏好,所以可以将Gumbel-Softmax变换随机值进行多次Co-Attention就可以得到他们的综合偏好 - 最终和自身的id特征进行拼接就是最终的
User和Item向量了$$X_u = [h_u,e^0_u,e^1_u,..,e^n_u],X_v = [h_v,e^0_v,e^1_v,..,e^n_v]$$ - 这些向量将会作为评分矩阵FM的输入以及文本序列生成GRU的初始化向量(可能会做一些MLP变换)
- 在最终的loss上有一个比较有意思的,除了传统词的NLL损失函数,还有一个属性的损失函数:$$L_c = \frac{1}{\Omega} \sum \sum (max (-\tau_k \text{log}o_{t,k}))$$ 这里$\tau$是用户和item偏好的评论属性向量,他们生成该文本总包含不评论属性,则做惩罚
总体上来说这边的初始化向量构造对比NRT合理了很多:
- 加入了用户信息的影响
- 同时引入了评论属性,这样生成文本时不容易偏移方向
还未细看
- 进行在线的解释生成:Dynamic Explainable Recommendation based on Neural Attentive Models
- 对抗学习进行解释生成:Why I like it: multi-task learning for recommendation and explanation.
- 根据多视角来进行解释生成:Explainable Recommendation Through Attentive Multi-View Learning
- 利用图像进行解释推荐:Visually-aware fashion recommendation and design with generative image models
- 使用bandit方法进行解释模板选择:Explore, Exploit, and Explain- Personalizing Explainable Recommendations with Bandits
总结
总体来说可解释方面的方向在学术上还是比较火热的,也有不少看上去比较可行的方案,但是实际迁移到工业界其实还是有不少的难度:
- 没有相应的训练数据
- paper:单个模型,实际业务:多个模型的融合/结合
- 透出的文本就算做到99%的相关性/准确性,剩下的1%都是要命的
参考
- Zhang, Yongfeng, et al. “Explicit factor models for explainable recommendation based on phrase-level sentiment analysis.” Proceedings of the 37th international ACM SIGIR conference on Research & development in information retrieval. ACM, 2014.
- Chen, Xu, et al. “Learning to rank features for recommendation over multiple categories.” Proceedings of the 39th International ACM SIGIR conference on Research and Development in Information Retrieval. ACM, 2016.
- Wang, Nan, et al. “Explainable recommendation via multi-task learning in opinionated text data.” The 41st International ACM SIGIR Conference on Research & Development in Information Retrieval. ACM, 2018.
- Chen, Chong, et al. “Neural attentional rating regression with review-level explanations.” Proceedings of the 2018 World Wide Web Conference. International World Wide Web Conferences Steering Committee, 2018.
- Li, Piji, et al. “Neural rating regression with abstractive tips generation for recommendation.” Proceedings of the 40th International ACM SIGIR conference on Research and Development in Information Retrieval. ACM, 2017.
- Chen, Zhongxia, et al. “Co-attentive multi-task learning for explainable recommendation.” Proceedings of the 28th International Joint Conference on Artificial Intelligence. Vol. 10. AAAI Press, 2019.
- ExplainAble Recommendation and Search
- https://blog.csdn.net/Y2c8YpZC15p/article/details/84801200

